Inhaltsverzeichnis
Nachfolgend werden die physikalischen Grundlagen, die zum Basiswissen eines Medizinphysik-Experten gehören, beschrieben. Um nicht den Rahmen dieser Seite zu sprengen, werden die Ausführungen auf das für die Klinik relevante Wissen reduziert. Wer Interesse an detailreicheren Erklärungen hat, findet diese sicher in der gängigen Fachliteratur. Beispielhaft nachfolgend einige empfehlenswerte Exemplare:
- W. Demtröder – Experimentelle Physik 4 (Kern-, Teilchen und Astrophysik)
- H. Krieger – Grundlagen der Strahlungsphysik und des Strahlenschutzes
- P. A. Tipler – Physik
- W. Schlegel – Medizinische Physik 2
- W. Schlungenbaum – Medizinische Strahlenkunde
- G. Goretzki – Medizinsiche Strahlenkunde
Das Atommodell
Zur Veranschaulichung und Darstellung der Wechselwirkungsprozesse wird im Folgenden das Bohrsche Atommodell verwendet, da es die hier relevanten physikalischen Beziehungen mathematisch korrekt darstellt und leicht zu verstehen ist. Wer Interesse an der Entwicklung des Modells, historischen Modellen z. B. nach Thomson oder Rutherford oder dem aktuellen anerkannten quantenphysikalischen Modell nach den Theorien von Schrödinger, Planck, Heisenberg, Einstein, Pauli, Fermi uvm. hat wird in der oben genannten Literatur fündig. Auf die Erklärung von quantenmechanischen Begriffen wie Orbitalen, Aufenthaltswahrscheinlichkeiten, Quantenzahlen und Drehimpulsen wird hier für Grundlagen folglich verzichtet.
Atome setzen sich aus einem kleinen Atomkern, bestehend aus positiv geladenen Protonen und neutralen Neutronen (Nukleonen) und der Atomhülle, bestehend aus negativ geladenen Elektronen, zusammen. Protonen und Neutronen sind mit einer Masse von ca. 1,67 ∙ 10-27 kg, 1840x schwerer als Elektronen, weshalb (fast) die gesamte Masse im Atomkern gebündelt ist. Die Elektronenwolke umgibt den Kern. Ihr Durchmesser beträgt ca. 10-10 m und ist damit ca. 10000x größer als der des Kerns. Befindet sich das Atom im Normalzustand, ist die Anzahl negativ und positiv geladener Teilchen identisch, wodurch das Teilchen nach außen hin neutral erscheint.
Die Elektronen bewegen sich vereinfacht dargestellt auf diskreten Bahnen um den Atomkern, wobei sie gegen das Verständnis der klassischen Physik, trotz der Bewegung auf der Kreisbahn, keine Energie abgeben.
Bohrsche Postulate (1913)
- Die Elektronen bewegen sich auf diskreten Bahnen mit festen Energien E_n. Dies sind die stationären Zustände des Atoms (Bohrsche Quantisierungsbedingung)
- Die Bewegung der Elektronen auf den Bahnen erfolgt strahlungsfrei. Der Übergang eines Elektrons auf eine Bahn mit geringerer Energie E_m ist möglich und geht mit der Emission von Strahlung mit der Frequenz f = (E_n – E_m) / h einher, wobei h das Planksche Wirkungsquantum ist. Die Strahlungsabsorption läuft analog auf inverse Weise ab.
- Für große Quantenzahlen n, m geht die Frequenzbedingung in die klassische Umlauffrequenz
\omega = v / 2r des Elektrons um den Kern über, wobei v die Umlaufgeschwindigkeit des Elektrons ist.

Bedingt durch die Coulombanziehung, variiert die Bindungsenergien der Elektronen je nach Schale (Elektronenbahn) bzw. Entfernung des Elektrons zum Atomkern sowie der Kernladungszahl. Die Kernladungszahl auch Ordnungs- oder Protonenzahl gibt die Anzahl der im Kern befindlichen Protonen bzw. bei elektrisch neutralen Atomen auch gleichzeitig die Anzahl der Elektronen an. Entsprechende Abhängigkeiten sind im Coulombschen Gesetz definiert. (Auch hier wird auf die quantenmechanische Erklärung verzichtet, weshalb sich die Protonen im Kern nicht abstoßen. Erläuterungen lassen sich in der bereits genannten Literatur finden). Pro Schale kann nur eine bestimmte Anzahl an Elektronen, nämlich 2n2 pro n-te Schalte, aufgenommen werden. Die Schalennamen sind Buchstaben, alphabetisch aufsteigend beginnend beim Buchstaben K. (Funfact: Der damalige Entdecker wusste nicht, ob es noch mehr Schalen gibt und ob sich diese näher oder weiter weg vom Atomkern befinden. Der Buchstabe liegt mittig im Alphabet und bietet damit ausreichend Platz in beide Richtungen).
Periodensystem / Nuklidkarte
Das populäre Periodensystem orientiert sich an der Ordnungszahl um chemisch ähnliche Atome in Gruppen darzustellen. Die einfachste Atomkonfiguration ist die des Wasserstoffatoms mit der Ordnungszahl 1. Es besteht aus einem Proton, das von einem sich auf der K-Schale befindlichen Elektron umkreist wird.
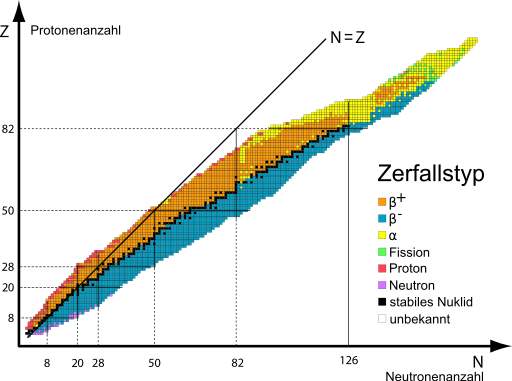
Genauso wichtig wie in der Chemie das Periodensystem, ist die Nuklidkarte in der Kernphysik. Die Nuklidkarte ist eine graphische Darstellung aller Nuklide, sortiert nach ihrer Protonen- und Neutronenanzahl. In der untenstehenden Nuklidkarte sind die unterschiedlichen Zerfallsarten farblich markiert. Anhand dessen ist erkennbar, dass aus der Anzahl sowie dem Verhältnis der Protonen- und Neutronenanzahl unterschiedliche Zerfallseigenschaften wie z. B. die Zerfallsart oder die Halbwertszeit resultieren.
Es gibt spezielle Atomarten die aufgrund ihrer Anzahl an Neutronen, Protonen oder Nukleonen zusammengefasst werden.
Isotope:
Gleiche Protonenzahl Z bei ungleicher Neutronenzahl N (z. B. C-12, C-13, C14. Allgemein: Waagerechte Linien in der Nuklidkarte)
Isotone:
Gleiche Neutronenzahl Z bei ungleicher Protonenzahl Z (z. B. C-12, N-13, O-14. Allgemein: Senkrechte Linien in der Nuklidkarte)
Isobare:
Gleiche Massenzahl bei ungleicher Protonen- und Neutronenzahl (z. B. C-12, N-12, B-12. Allgemein: Winkelhalbierende in der Nuklidkarte mit negativer Steigung)
Isodiaphere:
Gleiche Massenzahl bei ungleicher Protonen- und Neutronenzahl (z. B. C-12, N-12, B-12. Allgemein: Winkelhalbierende in der Nuklidkarte mit negativer Steigung)
Radioaktivität
Radioaktive Strahlung entsteht beim Zerfall instabiler Kerne unter Aussendung von Teilchen oder elektromagnetischer Strahlung. Die notwendige Bedingung für die Instabilität eines Kerns ist, dass die Masse der entstehenden Zerfallsprodukte kleiner als die des Mutterkerns ist (Energieerhaltung). Ein weiteres Kriterium ist die Parität von Neutronen- (N) und Protonenanzahl (Z) sowie deren Verhältnis zueinander. Daraus ergibt sich in der Nuklidkarte bzw. Z-N-Diagrammen die Anordnung der β+-, β- und α-Strahler sowie die der stabilen Kerne. Instabile Kerne laufen innerhalb der Nuklidkarte entlang ihrer Zerfallsketten, die ggf. weitere radioaktive Tochternuklide enthält Richtung stabile Kerne, die auf der Nuklidkarte „zwischen“ den instabilen Kernen liegen.
Der Zerfall radioaktiver Isotope erfolgt statistisch. Mit der Zerfallswahrscheinlichkeit \lambda lässt sich die Anzahl radioaktiver Kerne N in Abhängigkeit von der Zeit t darstellen.
N(t) = N_0 \cdot e^{-\lambda\cdot t}
N_0 bezeichnet die Anzahl der vorhandenen Kerne zum Zeitpunkt t=0. Die Zerfallswahrscheinlichkeit ist für jedes Nuklid konstant und größer, je instabiler das Isotop. Das Ableiten der Zerfallswahrscheinlichkeit liefert die Anzahl der zerfallenen Kerne pro Zeiteinheit.
A(t) = A_0 \cdot e^{-\lambda\cdot t}
Diese Größe heißt Aktivität und wird in der Einheit Becquerel (Bq = 1/s) angegeben. Historisch bedingt wird häufig noch die Einheit Curie (1 Ci = 37 GBq) verwendet. Analog ist hier A_0 die Aktivität zum Zeitpunkt t=0 . Eine weitere Wichtige Größe der Radioaktivität ist die Halbwertszeit T_{1/2} nach der die Hälfte aller Kerne N_0 zerfallen ist. Daraus resultiert N(T_{1/2}=N_0 / 2. Darüberhinaus gilt der folgende Zusammenhang zwischen der Halbwertszeit und der Zerfallskonstanten.
T_{1/2} = \frac{\ln(2)}{\lambda} \text{ bzw. noch allgemeiner } T_{1/n} = \frac{\ln(n)}{\lambda}
Beim Zerfall von Atomkernen wird zwischen drei Zerfallsarten differenziert, dem Alpha-, Beta- und Gammazerfall. Nachfolgend sollen diese kurz beschrieben werden. Eigentlich ist der Begriff „Zerfall“ nicht ganz korrekt, da teilweise nur Atomkern-Umwandlungen stattfinden. Der Einfachheit halber wird über diese fehlerhafte Begriffsdefinition hinweg gesehen.
Alpha-Zerfall
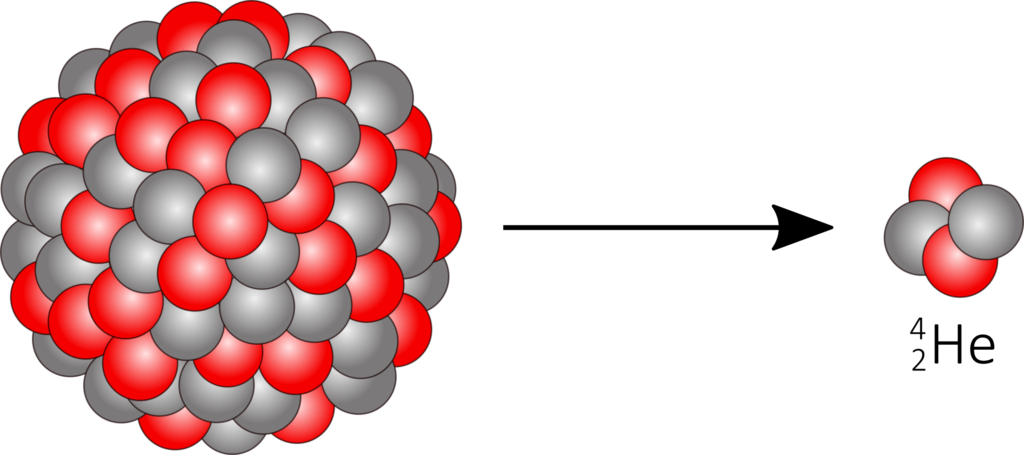
Beim α-Zerfall wird ein ionisierter Heliumkern vom zerfallenden Atomkern ausgesendet.
^A_Z\text{X} \longrightarrow ^{A-4}_{Z-2}\text{Y} + ^4_2\text{He}
Die Nukleonen im Kern werden durch das Kernpotential, das deutlich höher als die des α-Teilchens ist, zusammengehalten. Folglich ist eine Teilchenemission aus klassischer Sicht nicht möglich. Bei quantenmechanischer Betrachtung zeigt sich, dass eine Wahrscheinlichkeit besteht, dass Coulombpotential auch bei nicht ausreichender Energie zu „durchtunneln“. Die kinetische Energie des Teilchens resultiert aus der Coulomsabstoßung mit dem Atomkern, weshalb Alphazerfall-Spektren diskret sind. Aufgrund der elektrischen Ladung und der relativ hohen Masse des Heliumkerns, ist die Reichweite der α-Strahlung in Materie sehr gering.
Beta-Zerfall
Es existieren drei unterschiedliche Arten des β-Zerfalls. Die β+‑ und β—Umwandlung, resultierend aus Neutronenmangel und –überschuss, sowie der Elektroneneinfang (EC, für electron capture), der ebenfalls bei einem Neutronendefizit auftritt.
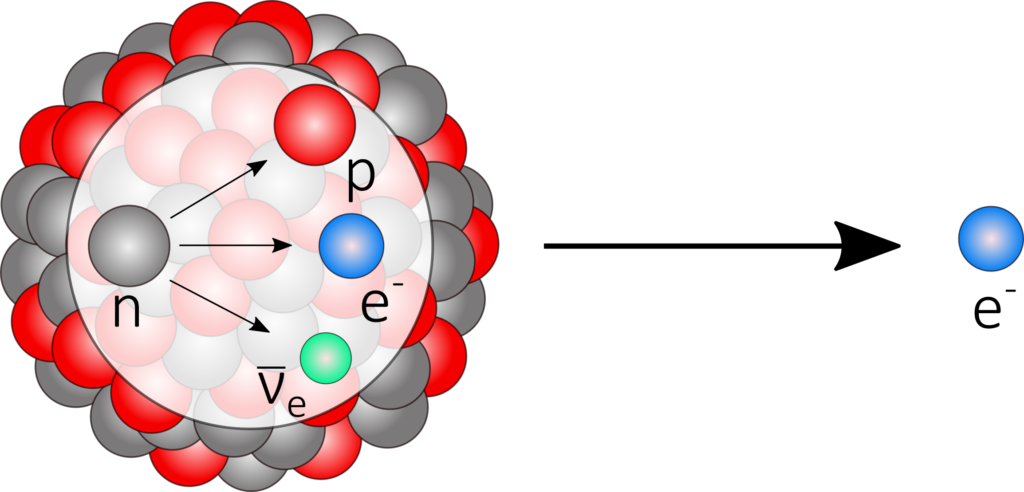
Als Folge eines Neutronenüberschusses wandelt sich ein Neutron unter Aussendung eines Elektrons sowie eines Elektron-Antineutrinos in ein Proton um. Die Kernladungszahl erhöht sich, während die Massenzahl konstant bleibt.
^A_Z\text{X} \longrightarrow ^A_{Z+1}\text{Y} + \text{e}^-+\bar\nu_e
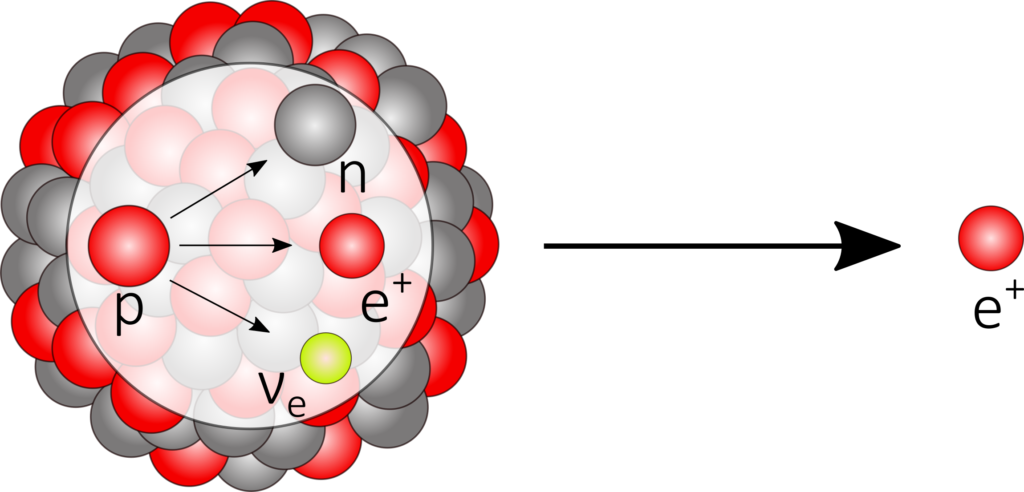
Liegt hingegen ein Neutronendefizit vor, wird die Anzahl durch die Emission eines Positrons und eines Elektron-Neutrinos erhöht. Dabei wandelt sich im Kern ein Proton in ein Neutron um, wobei die Kernladungszahl bei unveränderter Massenzahl sinkt.
^A_Z\text{X} \longrightarrow ^A_{Z-1}\text{Y} + \text{e}^+ +\nu_e
Zusätzlich finden bei allen β+‑Strahlern Elektroneneinfänge statt. In den meisten Fällen bildet ein Elektron der K-Schale mit einem Proton ein Neutron und ein Neutrino, welches abgestrahlt wird, weshalb der Prozess auch den Namen K-Einfang trägt.
^A_Z\text{X} + \text{e}^- \longrightarrow ^A_{Z-1}\text{Y} + \nu_e
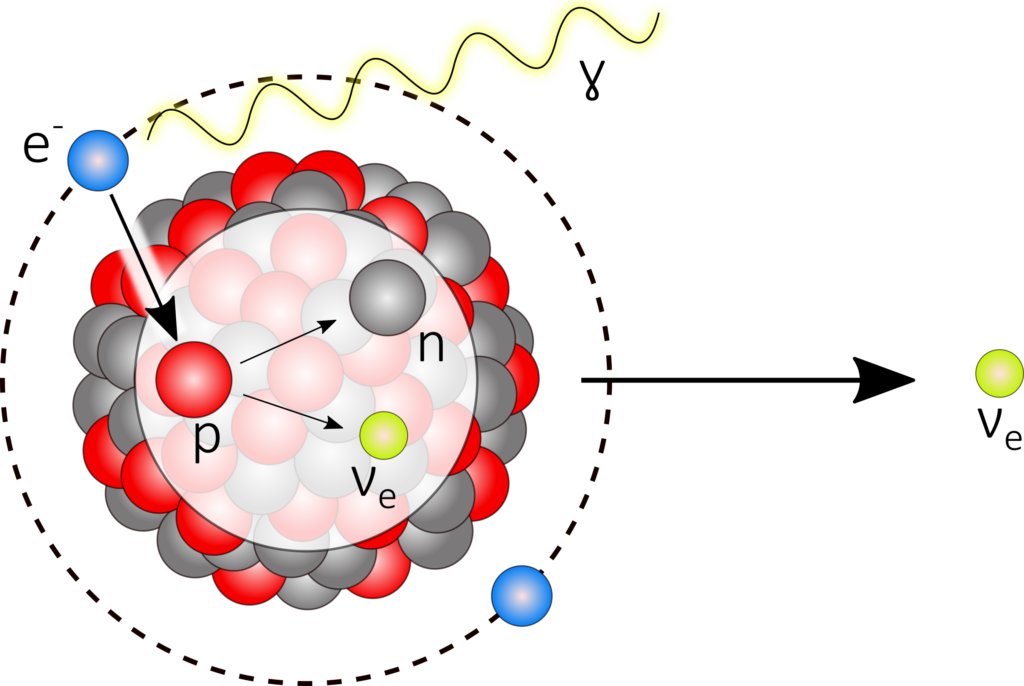
β‑Strahlung weist ein kontinuierliches Spektrum auf, da es sich bei dieser Zerfallsart nicht um ein Zweikörper-Zerfall, wie z. B. beim Alphazerfall, handelt. Die Reichweite der Elektronenstrahlung als größer als die eines α-Strahlers, da sowohl die Masse als auch die Ladung geringer ist. Neutrinos wechselwirken (fast) nicht mit Materie, weshalb sie für die Dosimetrie keine Rolle spielen (und sehr schwer nachweisbar sind).
Gamma-Zerfall
Nach einer Kernreaktion, z. B. in Folge eines Zerfalls, befindet sich der Kern oftmals in einem angeregten Zustand. Als Folgeprozess eine Atomkernanregung kommt es zur Emission von γ-Strahlung. Bedingt durch die diskreten Energiezustände ist auch das Spektrum eines Gamma-Strahlers diskret. Die Massenzahlen des Nuklids bleiben unverändert. Verglichen mit anderen Strahlungsarten ist die Reichweite der neutralen, masselosen γ-Quanten am höchsten.
Auger-Elektron
Der Auger-Effekt, benannt nach dem französischen Physiker Pierre Auger, ist ein quan-tenmechanisches Phänomen aus der Atomphysik. Er tritt auf, wenn die Energie eines Elektronenübergangs in einem Atom zum Herauslösen eines anderen Elektrons aus demselben System genutzt wird. Der Auger-Effekt tritt typischerweise in folgenden drei Schritten auf:
- Energiereiche Strahlung beispielsweise in Form von Photonen- oder Elektronenstrahlung, trifft auf ein Atom (in der Abbildung rot dargestellt) und gibt einen Teil seiner Energie ab. Dies führt dazu, dass ein Elektron auf einem inneren Schale des Atoms aus seinem Platz entfernt wird (in der Abbildung wird dieses Elektron nach unten herausgeschlagen).
- Ein Elektron aus einem höheren Energieniveau fällt in das leere Orbital des inneren Elektrons, um das entstandene Loch zu füllen (in der Abbildung von der L- auf die K-Schale). Dabei gibt es die Energiedifferenz wird genutzt (in der Abbildung durch gelbe Strahlung dargestellt), um ein charakteristischen Auger-Elektrons aus einer niederenergetischeren Schale herauszulösen (in der Abbildung aus der M Schale).
- Das ausgestoßene Auger-Elektron besitzt eine diskrete kinetische Energie Diese Energie hängt von den Energieniveaus der beteiligten Elektronen ab.
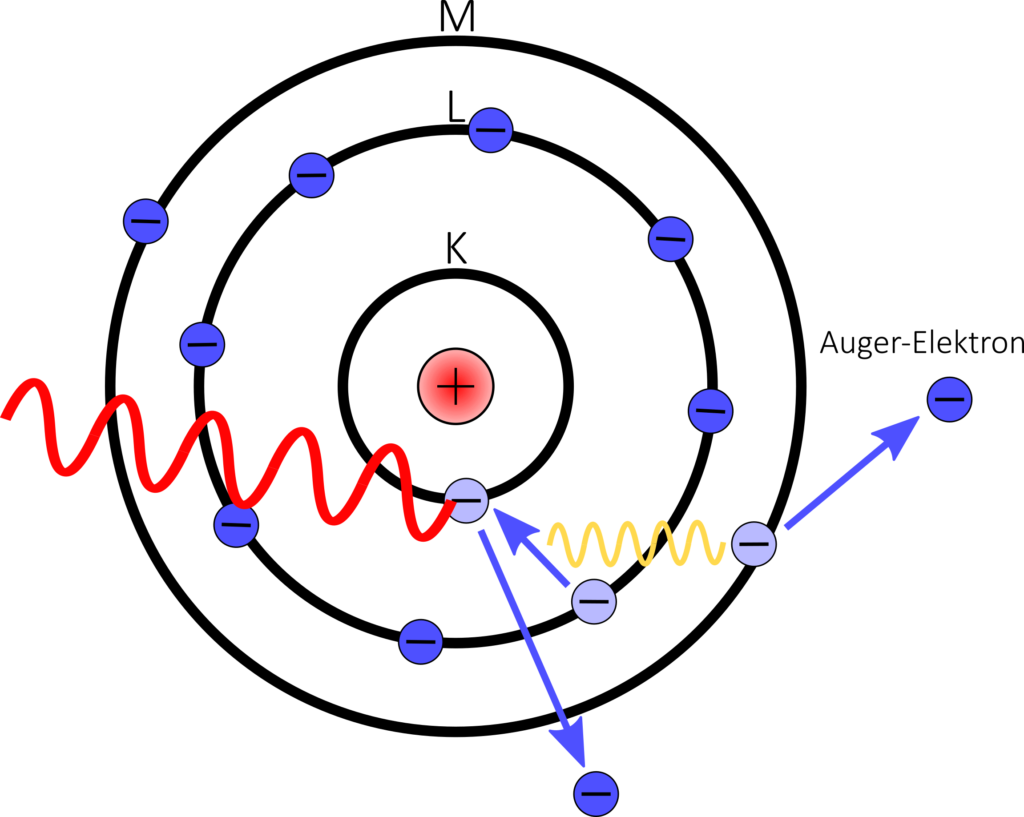
Statt die freiwerdende Energie zum Herauslösen eines Auger-Elektrons zu nutzen (Schritt 2), kann auch charakteristische Röntgenstrahlung entstehen. Dieser Vorgang ist folglich ein Konkurrenzprozess des Auger-Effekts.
Der Auger-Effekt ist von besonderer Bedeutung in der Röntgenspektroskopie, da er zur Identifizierung von Elementen und zur Bestimmung ihrer chemischen Zusammensetzung verwendet werden kann. Dies geschieht, indem die Energie und die Anzahl der ausgestoßenen Auger-Elektronen gemessen werden.