Inhaltsverzeichnis
Das übergeordnete Ziel der Bestrahlungsplanung ist die Applikation einer adäquaten Strahlendosis innerhalb des Zielvolumens (z.B. im Tumorgewebe) bei gleichzeitiger Schonung des Normalgewebes. Die Grundlage zur Umsetzung bilden die empirischen Dosiswirkungsbeziehungen für jede Tumorerkrankung, die die Wirkung und Nebenwirkungen in Abhängigkeit von der applizierten Dosis darstellen. Um eine konformale Dosisapplikation gewährleisten zu können, müssen definierte Qualitätssicherungsmaßnahmen eingehalten werden. Auf dieser Seite erfahrt ihr mehr über eine bestimmte Bewertungsmethodik in der patientenbezogenen Konstanzprüfung – die Gamma-Index-Analyse.
In Kapitel 7.2 der DIN 6875-3 wird bei fluenzmodulierten Bestrahlungen (IMRT) aufgrund der Komplexität des Verfahrens eine patientenbezogene Qualitätssicherung gefordert. Da eine Plausibilitätsprüfung der verwendeten Dosismonitorwerte – so wie sie in der konformalen 3D-Planung möglich ist – nur erschwert umsetzbar ist und der Aufbau der Feldsegmente für den Anwender nicht intuitiv bzw. zwingend nachvollziehbar ist, muss eine dosimetrische Prüfung des Bestrahlungsplans erfolgen. Zusätzlich wird dadurch sichergestellt, dass der Linearbeschleuniger den berechneten Plan im Rahmen definierter Toleranzen (dazu später mehr) umsetzt.
Zur Überprüfung der vom Bestrahlungsplanungsprogramm berechneten Dosisverteilung sind seit den 1990er Jahren mit der Einführung der intensitätsmodulierten Technik verschiedene Verifikationsmethoden entwickelt worden.
Historie
DD-Test
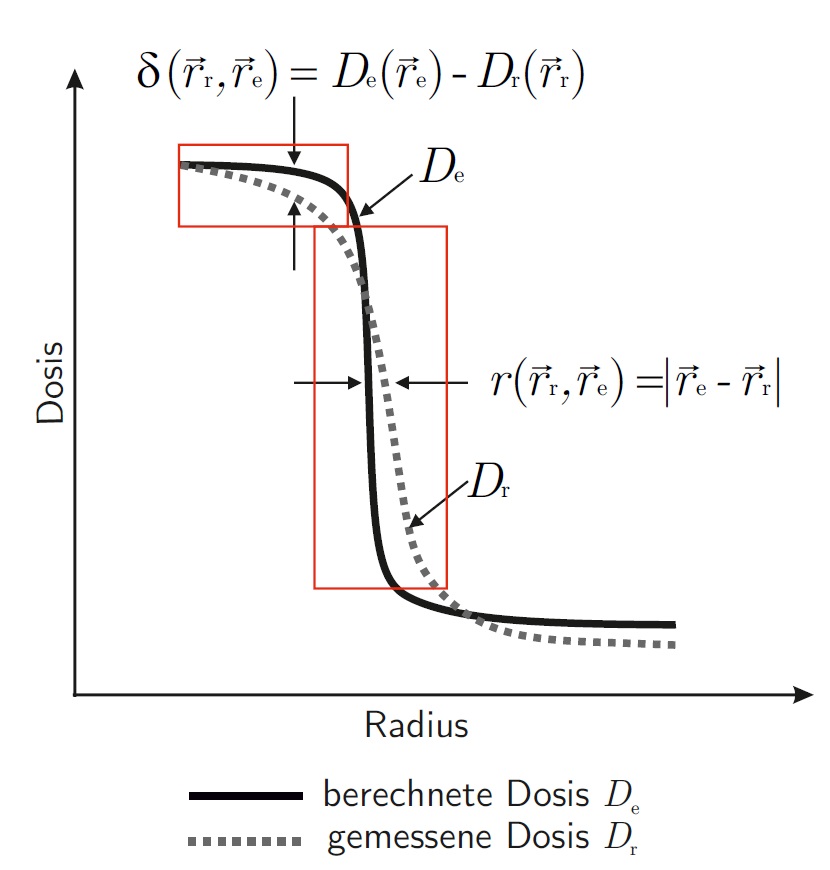
Beim DD-Test (engl. dose difference) wird bei absoluter Berechnung die Differenz \delta zwischen der vom Bestrahlungsplanungsprogramm berechneten Dosisverteilung D_\text{e} und der gemessenen Dosisverteilung D_\text{r} gebildet:
\delta(\vec r_\text{r}, \vec r_\text{e}) = D_\text{e}(\vec r_\text{e})\:-\:D_\text{r}(\vec r_\text{r})
Die Dosis D_\text{i}(\vec r_\text{i}) bezeichnet die Dosis an der Position \vec r_\text{i} . Statt der absoluten kann auch eine relative Betrachtung mithilfe einer Normierung vorgenommen werden. Vorteilhaft bei dieser Methode ist grundsätzlich die einfache Berechnung und Interpretation. Dennoch birgt diese Methode ein großes Risiko, wenn die zu vergleichenden Dosisverteilungen einen räumlichen Versatz zueinander aufweisen, insbesondere in einem Bereich mit einem steilen Dosisgradienten.
DTA-Test
Eine Optimierung der Planverifikation konnte mit der Einführung des sogenannten DTA-Tests (engl. distance to agreement) von Van Dyk et al. erzielt werden, der die ungefähre räumliche Differenz zwischen zwei Dosisverteilungen zurückgibt. Die Ortsdifferenz d(\vec r_\text{r}) ist der minimale Abstand zwischen einem Referenzpunkt und einem Punkt in der berechneten Dosisverteilung mit der gleichen Dosis.
d(\vec r_\text{e}) = \min{|\vec r_\text{r}\:-\:\vec r_\text{e}|} \: \forall \: {\vec r_\text{e}}
Im Vergleich zum DD-Test kann der DTA-Test sichere Resultate in Regionen mit steilem Dosisgradienten erzielen. Allerdings ist DTA-Methode wiederum in Regionen mit niedrigem Dosisgradienten ungeeignet. In der nachfolgenden Abbildung werden die Vor- und Nachteile beider Methoden schematisch dargestellt.
Composite-Test
Aufgrund der Nachteile der vorgestellten Verifikationsverfahren wurde ein binärer Pass-Fail-Test entwickelt, der Regionen identifiziert, in denen bestimmte Orts- und Dosiskriterien nicht erfüllt werden. Die binäre Composite-Verteilung wird aus den Punkten gebildet, die weder das DD-Kriterium \Delta D_\text{M} noch das DTA-Kriterium \Delta d_\text{M} erfüllen.
c(\vec r_\text{r} = 0) \text{ , falls } |\delta(\vec r_\text{r})| > \Delta D_\text{M} \cup |d(\vec r_\text{r})| > \Delta d_\text{M}
c(\vec r_\text{r} = 1) \text{ , falls } |\delta(\vec r_\text{r})| > \Delta D_\text{M} \cap |d(\vec r_\text{r})| \leq \Delta d_\text{M}
Ein Nachteil dieser Verifikationsmethode besteht jedoch darin, dass das binäre Ergebnis mit dem Wert 0 oder 1 lediglich angibt, ob die zu vergleichenden Dosisverteilungen den Composite-Test bestehen. Das Maß der Abweichung zwischen den Dosisverteilungen wird nicht quantifiziert.
Gamma-Index
Als Erweiterung der genannten Techniken schlugen 1998 Low et al. und 2002 Depuydt et al. einen Gamma-Index vor, der das DD- und das DTA-Kriterium in einer kontinuierlichen Verteilung vereint. Der Gamma-Wert ist ein Maß dafür, wie gut die berechnete mit der gemessenen Verteilung an einem bestimmten Messpunkt übereinstimmt.
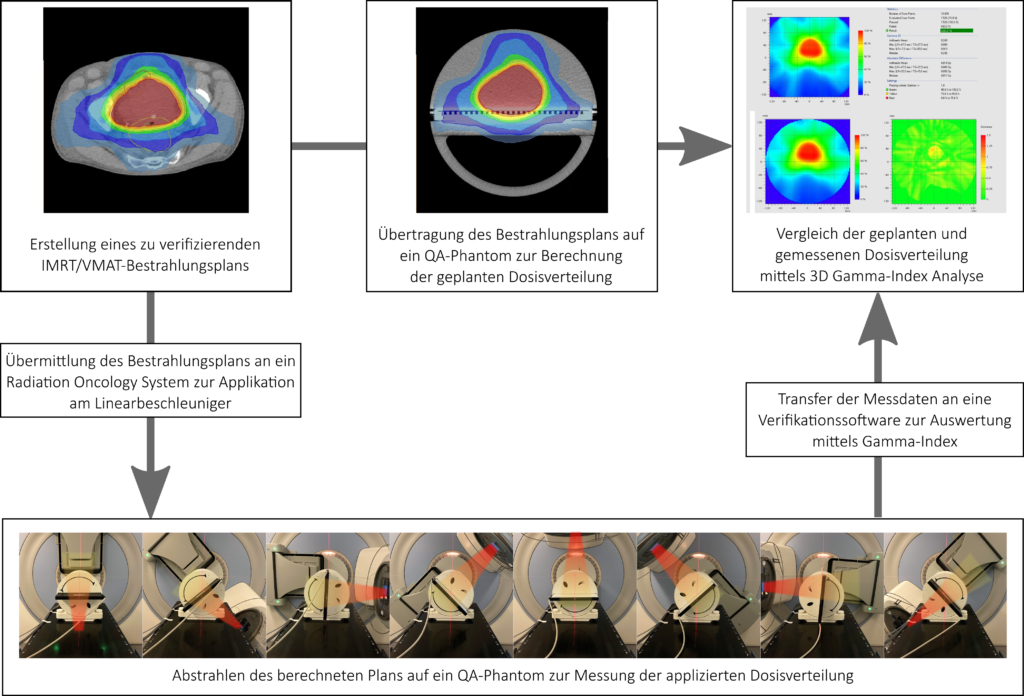
Heutzutage zählt der Gamma-Index-Test zum Goldstandard der Planverifikationsmethoden, um 2D- oder 3D-Dosisverteilungen miteinander zu vergleichen. Moderne Soft- und Hardware ermöglichen die Berechnung von 3D-Dosisverteilungen, die mithilfe von aus verschiedenen Winkeln gemessenen 2D-Matrizen rekonstruiert werden.
Berechnung
Der Gamma-Wert steigt sowohl mit der Ortsdifferenz DTA als auch mit der Dosisdifferenz DD zwischen gemessenen und berechneten Werten an. Nach den Kriterien, die von Harms et al. definiert wurden, wird bei einem Berechnungspunkt, der exakt an derselben Stelle liegt ( d(\vec r_\text{r}) = 0 ), aber eine Dosisdifferenz von \delta(\vec r_\text{r}, \vec r_\text{e}) \geq \Delta D_\text{M} , aufweist, ein Wert von 1 angenommen. Analog nimmt der Gamma-Wert in einem Punkt, in dem zwar die Dosiswerte identisch sind ( \delta(\vec r_\text{r}, \vec r_\text{e}) = 0 ), aber die Distanz größer als das Ortskriterium ( d(\vec r_\text{r}) \geq \Delta d_\text{M} ) ist, den Wert 1 an.
Es gilt der folgende Zusammenhang:
\Gamma(\vec r_\text{r}, \vec r_\text{e}) = \sqrt{\frac{r^2(\vec r_\text{r}, \vec r_\text{e})}{\Delta d^2_\text{M}} + \frac{\delta^2(\vec r_\text{r}, \vec r_\text{e})}{\Delta D^2_\text{M}}}
Mathematisch beschreibt die Formel den skalierten, minimalen euklidischen Abstand zwischen einer berechneten Verteilung und jedem Punkt der gemessenen Dosisverteilung. Die DTA-Dimension wird wieder durch
r(\vec r_\text{r}, \vec r_\text{e}) = | \vec r_\text{e} \: – \: r_\text{r} |
festgelegt. Die DD-Dimension über
\delta (\vec r_\text{r}, \vec r_\text{e}) = D_\text{e}(\vec r_\text{e}) \: – \: D_\text{r}(\vec r_\text{r}) .
Beispiel: Beträgt der Abstand des berechneten und gemessenen Punkt r(\vec r_\text{r}, \vec r_\text{e}) = \Delta d_\text{M}/2 und die Dosisdifferenz \delta (\vec r_\text{r}, \vec r_\text{e}) = \Delta D_\text{M}/2 , so gibt \Gamma-Funktion den Wert 1 / \sqrt{2} = 0,71 wieder.
Die Kriterien \Delta D_\text{M} und \Delta d_\text{M} legen im örtlich eindimensionalen Dosisprofil die Hauptachsen einer Ellipse und im örtlich zweidimensionalen Dosisprofil die Hauptachsen eines Ellipsoiden fest, wie in den nachstehenden Abbildungen zu sehen.
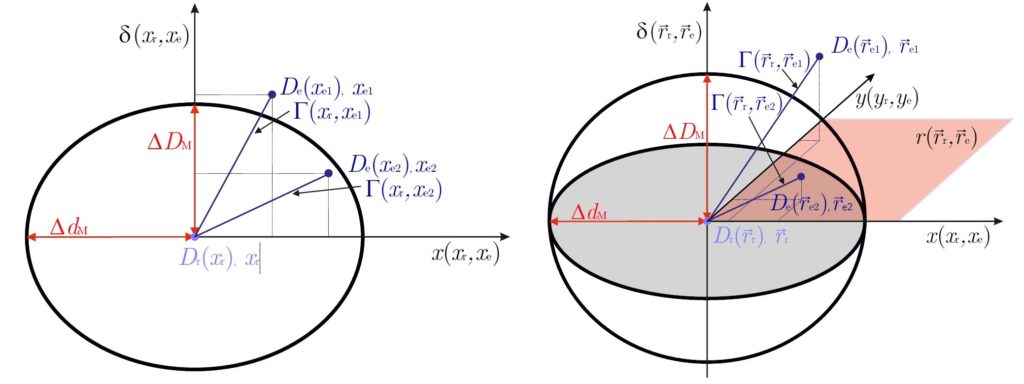
Jeder Punkt \vec r_\text{r} des Referenzgitters, d. h. der gemessenen Verteilung, wird Zentrum einer solchen Ellipse oder Ellipsoids. Für alle Punkte \vec r_\text{e} der berechneten Dosisverteilung wird dann der \Gamma-Wert bestimmt. Sofern sich der jeweilige berechnete Dosispunkt in der Ellipse/im Ellipsoid befindet, erfüllt dieser das DTA- und das DD-Kriterium und der \Gamma-Wert ist kleiner als 1. Wenn weder das DTA- noch das DD-Kriterium erfüllt ist, liegt der Wert über 1 und der Punkt außerhalb der Ellipse/des Ellipsoids. Aus allen berechneten \Gamma-Werten (für jeden Punkt) wird der finale, minimale Gamma-Wert \gamma(\vec r_\text{r})-Wert für alle Punkte \vec r_\text{r} ermittelt:
\gamma(\vec r_\text{r}) = \min(\Gamma(\vec r_\text{r}, \vec r_\text{e}) \: \forall \: {\vec r_\text{e}})
Eine Klassifizierung des Gamma-Index-Test erfolgt schlussendlich über das binäre Kriterium:
- \gamma(\vec r_\text{r}) \leq 1\text{ : Test bestanden.}
- \gamma(\vec r_\text{r}) > 1\text{ : Test nicht bestanden.}
Je kleiner der \gamma-Wert bzw. je mehr Prüfungen das Pass-/Fail-Kriterium bestanden haben, desto besser stimmt die gemessene und berechnete Dosisverteilung für den jeweiligen Messpunkt überein. Über ein \gamma-Histogramm oder eine 2D-\gamma-Verteilung kann der Anwender einsehen, in welcher Anzahl welche \gamma-Werte erreicht wurden und in welchen Regionen die beiden Verteilungen wie stark voneinander abweichen. Werte, die größer als eins sind, liefern beim Gamma-Index-Test allerdings keine Auskunft über die Ursache der Abweichung.
Kriterien
Die Orts- und Dosiskriterien \Delta d_\text{M} und \Delta D_\text{M} werden vom Anwender festgelegt. Verbreitet ist die klinische Freigabe, wenn mindestens 95% (Gamma-Passing-Rate) der Punkte die Kriterien \Delta d_\text{M} = 3\:\text{mm} und \Delta D_\text{M} = 3\: \% erfüllen. Diese Kriterien definieren die zulässige Abweichung, wobei die jeweils maximale Abweichung nur akzeptiert wird, sofern das jeweils andere Kriterium genau identisch ist. Häufig werden auch die Kriterien 2mm/2%, 3mm/2% oder 2mm/3% verwendet. Bei stereotaktischen Bestrahlungen, insbesondere in der Single-Fraction-Radiotherapie (SFRT), ist ein strengeres Ortskriterium (z.B. 1mm/3%) empfehlenswert. Um bei VMAT-Plänen potenzielle MLC-Fehler zu identifizieren, empfahlen Heileman et al. 2018 die Verwendung der Kriterien \Delta d_\text{M} = 2\:\text{mm} und \Delta D_\text{M} = 2\:\% und eine Passing-Rate von über 90%.
Da im Niedrigdosisbereich sehr schnell große relative Dosisdifferenzen entstehen, die das Ergebnis verfälschen könnten, ist die Definition einer Schwellendosis sinnvoll. Es ist üblich, die \gamma-Berechnung auf Punkte zu beschränken, deren Dosis größer als 10 – 20 % der maximalen Dosis innerhalb der Verteilung ist.
Lokaler und globaler Gamma-Index
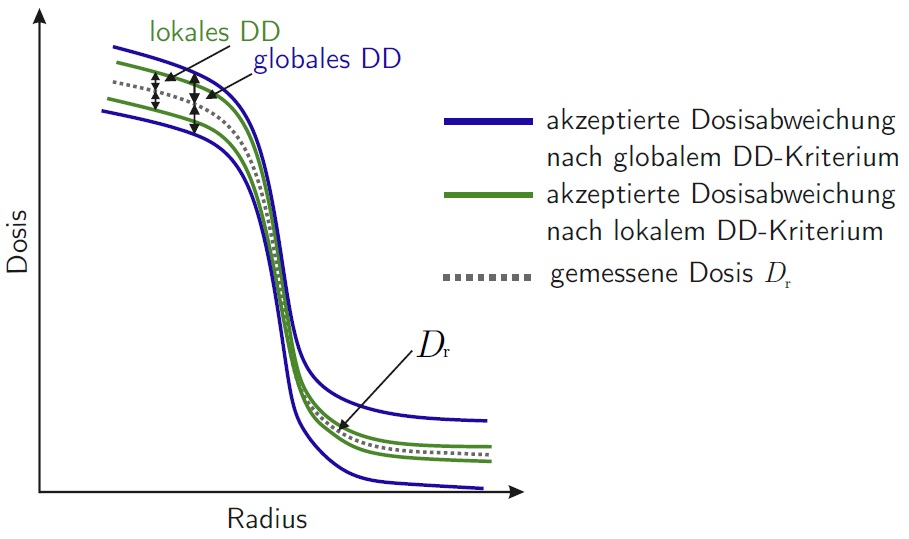
Die \gamma-Berechnungen können entweder lokal oder global ausgewertet werden. Beim lokalen Test wird die Dosisabweichung für jeden einzelnen Dosispunkt der Referenzverteilung festgelegt. Für eine globale Betrachtung ändert sich die Dosisdifferenz zu
\delta(\vec r_\text{r}, \vec r_\text{e}) = (D_\text{e}(\vec r_\text{e}) – D_\text{r}(\vec r_\text{r})) / D_\text{norm} .
Die Normierungsdosis D_\text{norm} kann unterschiedlich definiert werden, z. B. als die maximale Dosis innerhalb der Referenzdosisverteilung D_\text{r}(\vec r_\text{r}) oder als Punkt in Hochdosisbereichen mit kleinem Gradienten, sodass sich für alle Punkte der gemessenen Dosisverteilung eine konstante, absolute akzeptierte Messabweichung ergibt.
Der lokale Test ( \gamma_\text{lokal} ) hebt tendenziell Inkongruenzen zwischen berechneter und gemessener Dosisverteilung in Regionen mit hohem Dosisgradienten und in Regionen niedriger Dosis hervor, während der globale Test ( \gamma_\text{global} ) eher Inkongruenzen in den Regionen mit höherer Dosis innerhalb der Dosisverteilung aufzeigt. Die lokale Berechnung ist daher eher für eine kritischere Planverifikation zu verwenden, da insbesondere Abweichungen im Niedrigdosisbereich, in dem z.B. Risikoorgane lokalisiert sein können, in die Planbewertung miteinbezogen werden. Insgesamt ist die Wahl der lokalen oder globalen Berechnungsmethode davon abhängig, welche internen Anforderungen an die Verifikationsmethode gestellt werden. Für die Interpretation der Ergebnisse ist es entscheidend zu wissen, welche Methode angewendet wurde. Sollte die Wahl auf den globalen Index fallen, ist die Wahl der Normierungsdosis ebenso entscheidend.
Kritische Literatur
Obwohl die Gamma-Index-Analyse heutzutage in den meisten Kliniken der Standard zur Verifikation und Freigabe von Bestrahlungsplänen ist, existieren keine einheitlichen Vorgaben hinsichtlich des DD- und DTA-Kriteriums sowie der anzustrebenden Gamma-Passing-Rate. Folglich ist es dem Anwender überlassen, sinnvolle Kriterien zu definieren.
Erschwert wird diese Aufgabe, durch Herausforderungen wie z. B. die Art der Interpolation oder die Berücksichtigung der Auflösung der berechneten 2D- oder 3D-Dosisverteilungen. Fredh et al. und Hussein et al. haben 2013 eine Abhängigkeit des Index vom verwendeten QA-System herausgefunden, da je nach Detektor unterschiedliche Fehler identifiziert werden können. Die Gamma-Passing-Rate hängt also vom verwendeten Dosimeter-Typ ab.
2011 versuchten Nelms et al. die Korrelation zwischen der Gamma-Passing-Rate und Dosisabweichungen (z.B. in OAR) zu bestimmen. Diese Arbeit zeigte, dass eine niedrigere oder höhere Dosis in relevanten ROIs nicht zwingend zu niedrigeren Akzeptanzraten bei der Gamma-Index-Analyse geführt haben.
Park et al. untersuchten 2018 die Verlässlichkeit des Gamma-Index für VMAT-Verifikationen in Abhängigkeit der definierten Toleranzkriterien, des verwendeten Linearbeschleunigers und QA-Systems bzw. des Dosimeters. Auch hier zeigte sich, dass die Passing-Rate je nach Setup variierte.
Es bleibt festzuhalten, dass der Gamma-Index– neben der Erfüllung der Anforderungen der DIN 6875-3 – als Indikator für Probleme in Bestrahlungsplänen verwendet werden sollte, jedoch nicht einzig zur Beurteilung der Planqualität.
Gastbeitrag - Danksagung
Die Grundlage für diesen Artikel stammt aus der Masterarbeit von Fr. Feline Heinzelmann, aus der in Zusammenarbeit mit der TU Dortmund und dem Gamma-Knife Zentrum Bochum auch die Publikation „Evaluation of a new inverse, globally convex TPS algorithm for Gamma Knife® radiosurgery within a prospective trial – advantages and disadvantages in practical application“ (Advandes in Radiation Oncology, 2022) resultiert ist.
Wir bedanken uns für diesen tollen Gastbeitrag!
Weiterführende Literatur
- S. Diamantopoulos, K. Platonia, G. Patatoukasa et al., „Treatment plan verification: a review on the comparison of dose distributions“ (2019)
- S. B. Jiang, G. C. Sharp, T. Neicu et al., „On dose distribution comparison“, Physics in medicine and biology 51, 759–776 (2006)
- J. Van Dyk, R. B. Barnett, J. E. Cygler et al., „Commissioning and quality assurance of treatment planning computers“, International Journal of Radiation Oncology, Biology, Physics 26, 10.1016/0360-3016(93)90206-b (1993)
- W. B. S. Harms, D. A. Low, J. W. Wong et al., „A software tool for the quantitative evaluation of 3d dose calculation algorithms“, Medical Physics 25, 10.1118/1.598363 (1998)
- Nelms BE, Zhen H, Tome WA, “Per-beam, planar IMRT QA passing rates do not predict clinically relevant patient dose errors”, Medical Physics (2011)
- D. A. Low, W. B. Harms, S. Mutic et al., „A technique for the quantitative evaluation of dose distributions“, Medical Physics 25, 656–661 (1998)
- T. Depuydt, A. Van Esch, D. Pierre Huyskens, „A quantitative evaluation of IMRT dose distributions: refinement and clinical assessment of the gamma evaluation“, Radiotherapy and Oncology 62, 309–319 (2002)
- M. Hussein, P. Rowshanfarzad, M. A. Ebert et al., „A comparison of the gamma index analysis in various commercial IMRT/VMAT QA systems“, Radiotherapie and Oncology 109(3) (2013)
- Fredh, J. B. Scherman, L. S. Fog et al., „Patient QA systems for rotational radiation therapy: a comparative experimental study with intentional errors”, Medical Physics 40(3), (2013)
- J. M. Park et al., “Reliability of the gamma index analysis as a verification method of volumetric modulated arc therapy plans”, Radiation Oncology (2018)
- J. Kim et al., “The sensitivity of gamma-index method to the positioning errors of high-definition MLC in patient-specific VMAT QA for SBRT”, Radiation Oncology (2014)