Röntgenröhre / Röntgenstrahlung · Medizinische Physik

Röntgenquelle

Bei den bildgebenden Verfahren der Röntgendiagnostik wird elektromagnetische Strahlung in einem Energiebereich von circa 30 keV bis 150 keV verwendet, die zu Ehren ihres Entdeckers, Wilhelm Conrad Röntgen, auch als „Röntgenstrahlung“ bezeichnet wird. Im Gegensatz zur Gammastrahlung entsteht die Röntgenstrahlung nicht bei Kernreaktionen, sondern durch die Geschwindigkeitsänderung geladener Teilchen (i. A. Elektronen). In der Röntgendiagnostik wird die Röntgenstrahlung durch Abbremsung energiereicher Elektronen in sogenannte Röntgenröhren erzeugt.

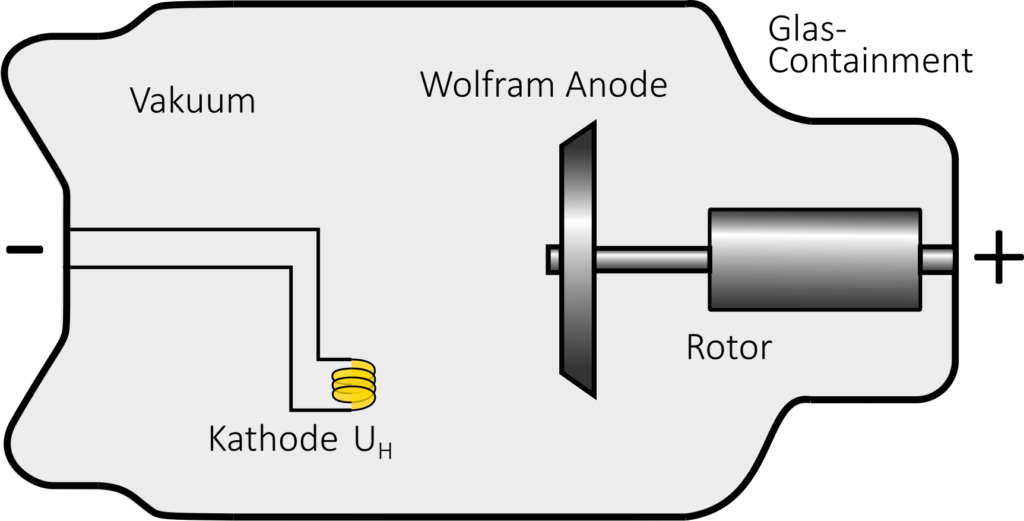
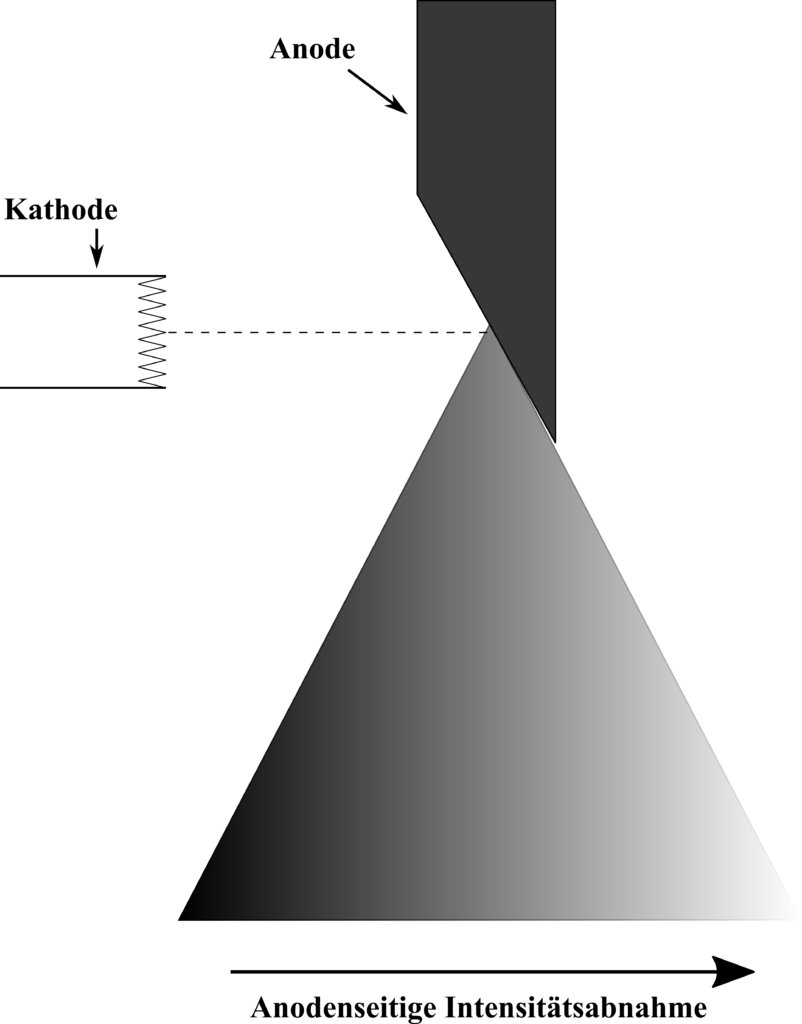
Grundsätzlich besteht eine Röntgenröhre aus einer Heizkathode und einer drehbar gelagerten Anode, die sich beide in einem evakuierten Containment aus Glas oder einer Metall-Keramik-Verbindung befinden (s. Abbildung). Durch eine Ölfüllung zwischen Schutzgehäuse und Röhre kann der Hochspannungsschutz gewährleistet und die abgestrahlte Wärme aufgenommen werden. Als Anodenmaterial hat sich für die aller meisten Anwendungen eine Wolfram-Rhenium Legierung bewährt. Eine Ausnahme bilden Röntgenquellen, die bei der Mammographie eingesetzt werden. Zur Darstellung des Weichteilkontrastes wird ein charakteristisches Röntgenspektrum von unter 20 keV verwendet, das sich am besten mithilfe von Molybdänanoden erzeugen lässt.

Erzeugung der Röntgenstrahlung

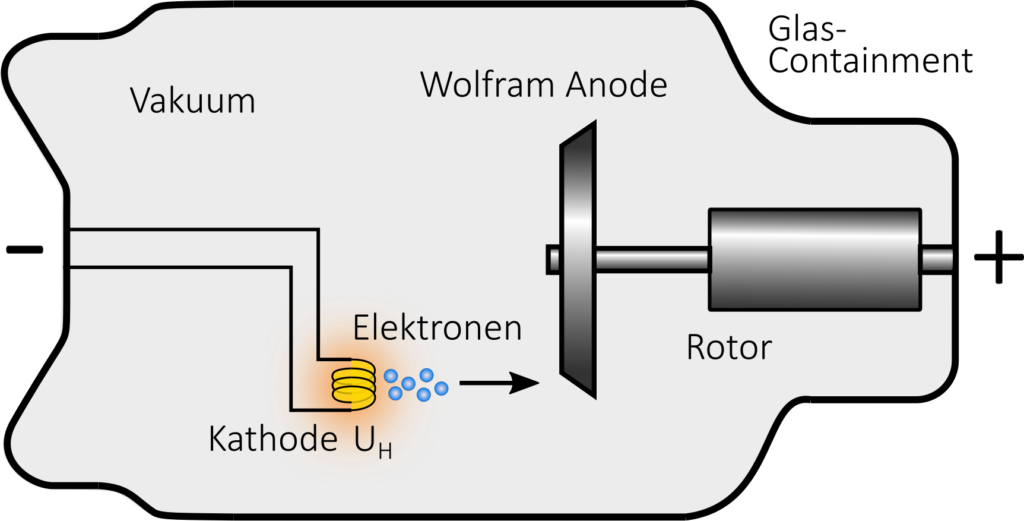
Die Kathode einer Röntgenröhre besteht aus einer Glühwendel, die durch das Anlegen einer Heizspannung $U_H$ von einigen Volt auf eine Temperatur von circa 2.000 K geheizt wird. Durch den thermoelektrischen Effekt können nun schwach oder gar nicht gebundene Elektronen freigesetzt werden. Die dafür benötigte Energie wird Austrittsarbeit genannt. Das Kathodenmaterial muss also hitzebeständig sein und zugleich eine möglichst geringe Austrittsarbeit besitzen. Für die meisten Anwendungen hat sich mit einem Thoriumfilm bedampftes Wolfram bewährt. Die Schmelztemperatur von Wolfram ist mit 3.695 K relativ hoch und die Austrittsarbeit von Thorium mit 2,8 eV relativ klein (Krieger, Strahlungsquellen für Technik und Medizin, 2012). Der entstehende Röhrenstrom $I_A$ (freigesetzte Ladungen pro Zeit) kann durch Anpassung der Heizspannung variiert werden.

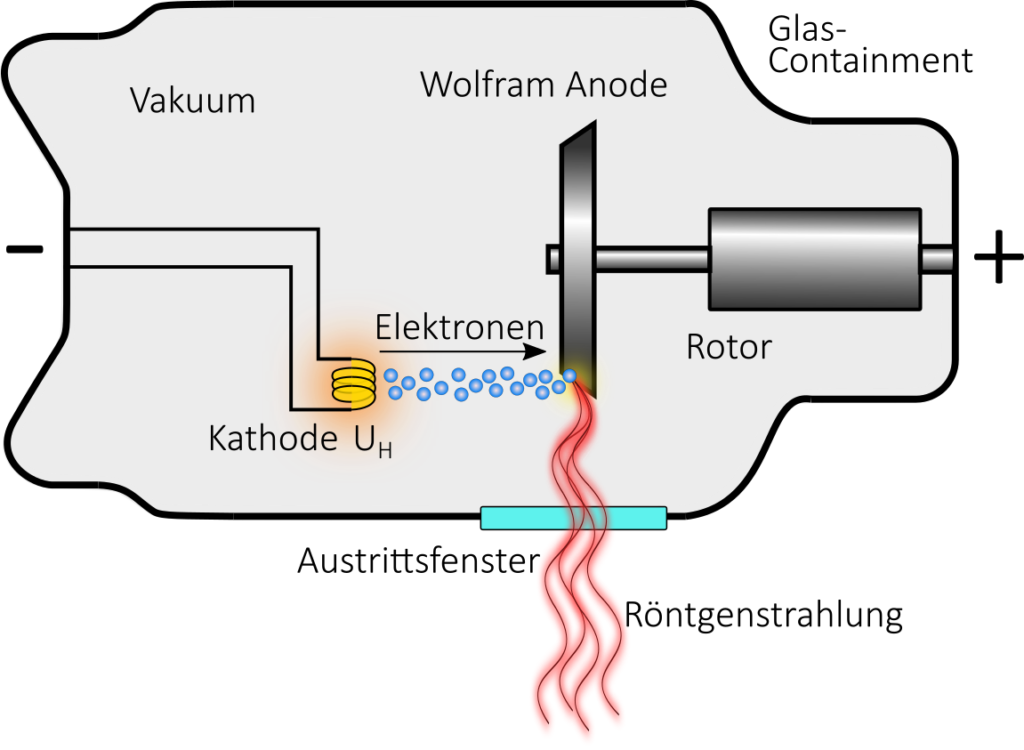
Durch Anlegen einer Anodenspannung $U_A$ zwischen Kathode und Anode werden die freigesetzten Elektronen zur Anode beschleunigt. Die Anodenspannung wird von einem Generator zur Verfügung gestellt. Handelt es sich um einen gleichrichtenden Wechselspannungsgenerator kann eine sog. Restwelligkeit (engl. $\text{ripple}$ ) bestehen. Dabei handelt es sich um die prozentuale Differenz zwischen maximaler $\text{kV}_\text{p}$ und minimaler $\text{kV}_\text{min}$ Spannung während einer Periode:

$\text{ripple} = (\text{kV}_\text{p} – \text{kV}_\text{min}) / \text{kV}_\text{p}$

In diesem Fall wird die Maximalspannung (engl. peak-tube-voltage) $\text{kV}_\text{p}$ angegeben (s. Abbildung). Durch die auf eine Energie von $\text{e} \cdot U_\text{A}$ beschleunigten Elektronen kommt es im Anodenmaterial durch zwei wesentliche Effekte zur Entstehung von Röntgenstrahlung, deren Überlagerung emittierte Röntgenspektrum bilden.

Bremsstrahlung

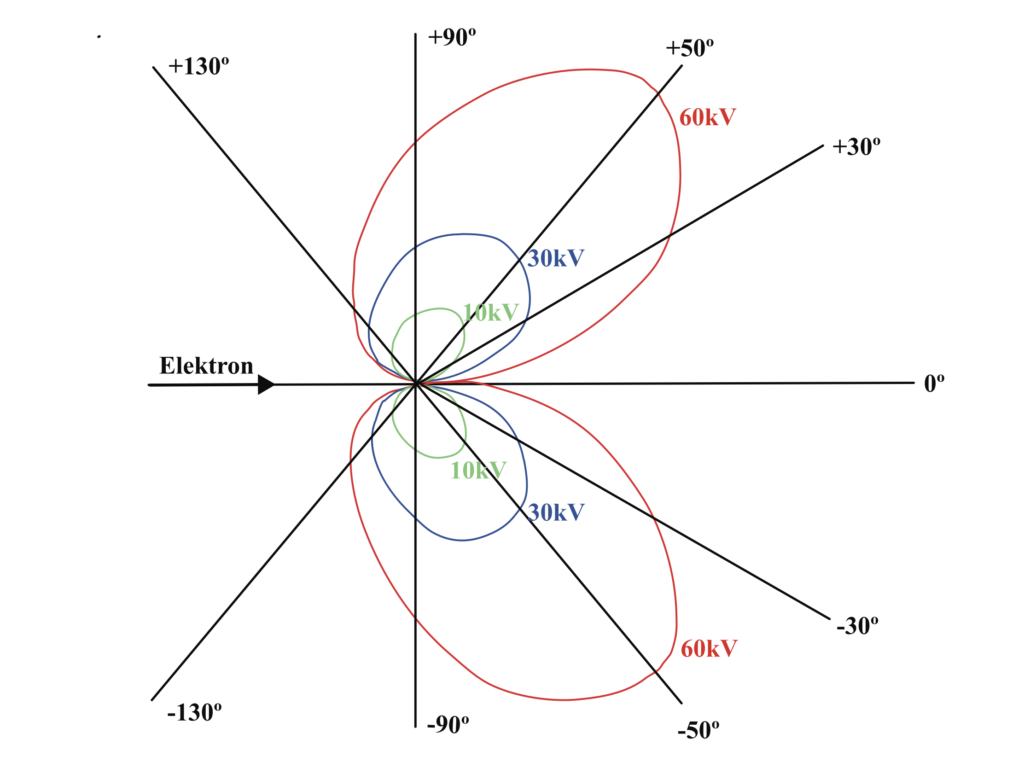
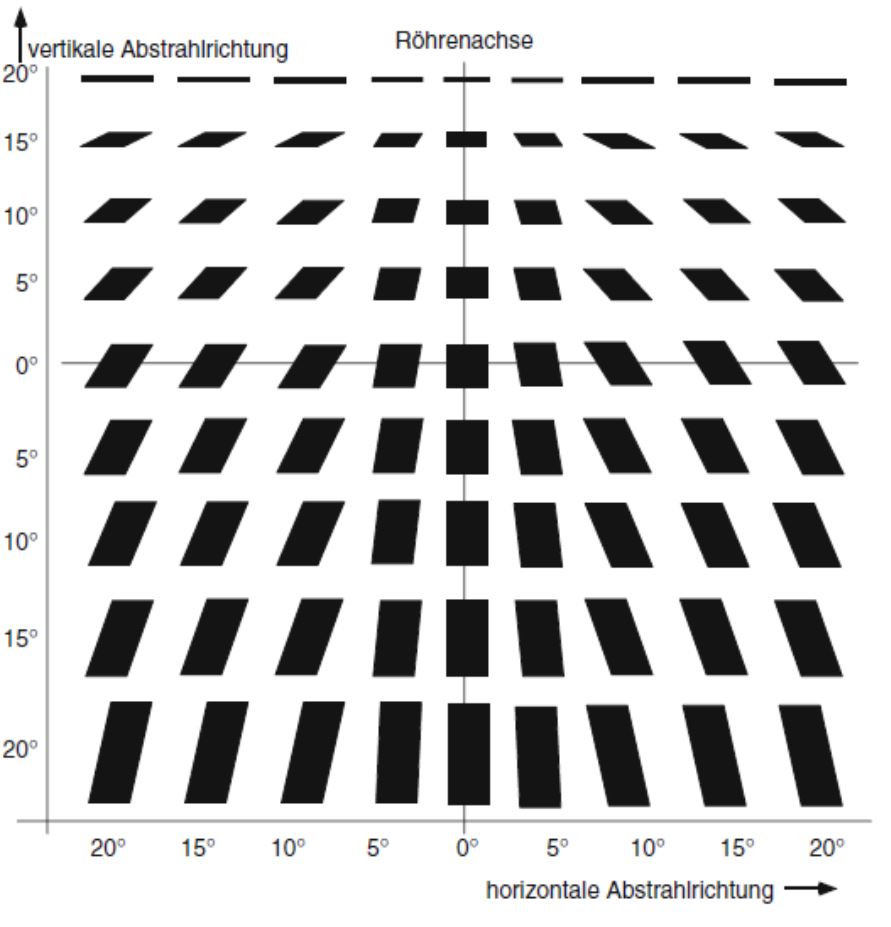
Die Elektronen im Coulombfeld der Atomkerne in der Anode abgelenkt, wodurch es zur Emission von Bremsstrahlung kommt. Die Photonenenergie h·f entspricht der Energiedifferenz des Elektrons vor und nach der Wechselwirkung. Die Energieverteilung der so emittierten Photonen ist kontinuierlich und die räumliche Intensitätsverteilung ist vergleichbar mit der Form eines Hertzschen Dipols, dessen „Strahlungskeulen“ durch relativistische Effekte umso weiter in Bewegungsrichtung verbogen sind, je größer die Anodenspannung gewählt ist (s. Abbildung unten links). Aufgrund der Vielzahl von Wechselwirkungen in unterschiedlichen Bewegungsrichtungen hebt sich dieser Effekt jedoch weitestgehend auf, sodass die resultierende räumliche Intensitätsverteilung des Bremsspektrums nahezu isotrop ist. Einzig der Winkelbereich, der fast parallel zur Anodenoberfläche liegt, besitzt eine geringere Intensität. Grund dafür ist die Selbstabsorption der entstehenden Röntgenstrahlung durch das Anodenmaterial. Dies wird „Heel-Effekt“ genannt (s. Abbildung unten rechts).

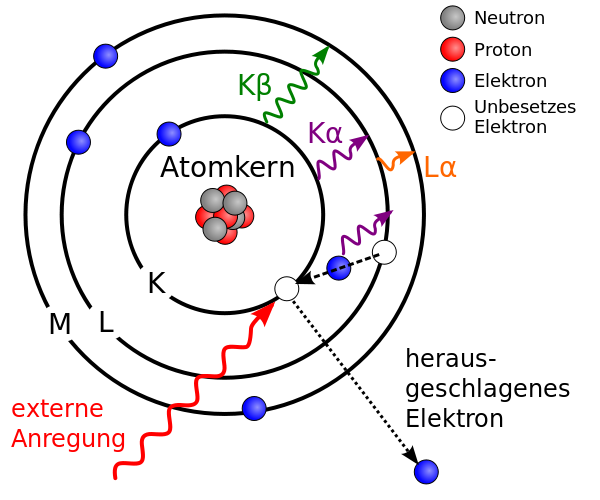
Charakteristische Röntgenstrahlung

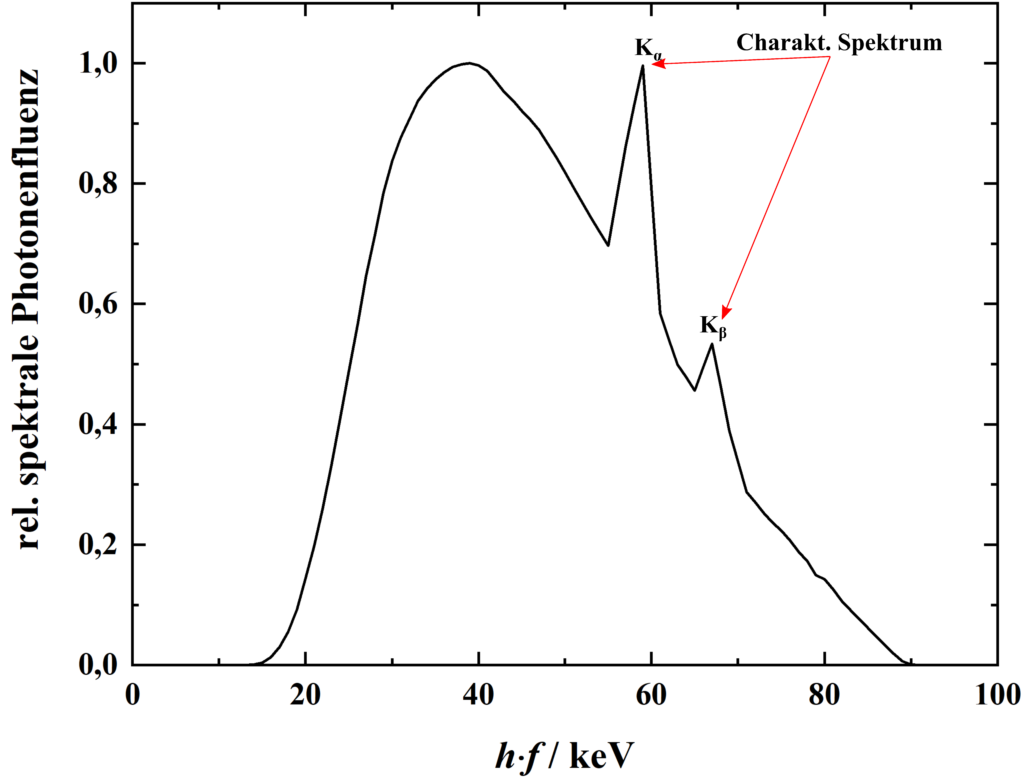
Durch Wechselwirkungen zwischen den einfallenden Elektronen (oder den Bremsstrahlungs-Photonen) und den Hüllenelektronen des Anodenmaterials werden Elektronen aus den inneren Energieniveaus (K-Schale, L-Schale etc.) gelöst und die Atome so angeregt oder ionisiert. Das anschließende Auffüllen der Lücke durch ein Elektron aus einem höheren Niveau kann zur Emission von Röntgenstrahlung führen. Das so emittierte Spektrum ist diskret und wird auch charakteristisches Röntgenspektrum genannt, da die emittierten Energien spezifisch für das Anodenmaterial sind.

In der Abbildung unten rechts ist ein solches Röntgenspektrum exemplarisch dargestellt.

Qualitätskriterien von Röntgenquellen

Wirkungsgrad

Der Quotient aus Röntgenleistung und elektrischer Leistung definiert den Wirkungsgrad $\eta$ . Dieser liegt typischerweise zwischen 0,5 % und 1 %. Die restliche Bewegungsenergie wird in Wärme umgesetzt. Der Wirkungsgrad ist proportional zur Anodenspannung und Kernladungszahl $Z$ des Anodenmaterials. Außerdem sollte das Anodenmaterial aufgrund der starken Wärmeentwicklung eine hohe Wärmeleitfähigkeit $\lambda$ und Schmelztemperatur $T_\text{max}$ aufweisen. Das Produkt

$Z \cdot \lambda \cdot T_\text{max}$

dient somit als Qualitätsmaß für das Anodenmaterial. Auch hier liefert Wolfram in aller Regel die beste Lösung. Durch Hinzufügen einer kleinen Menge Rhenium kann zudem die Aufrauhung verzögert und so die Lebensdauer erhöht werden. Die Wolfram-Rhenium-Mischung wird auf einen Sockel aus Molybdän und Graphit aufgetragen. Molybdän und Graphit sind leicht zu verarbeiten und besitzen eine noch höhere spezifische Wärmekapazität als Wolfram. Somit können Anoden hergestellt werden, die eine Energie von 10⁶ Ws aufnehmen können, bevor sie Schaden nehmen.

Größe des optischen Brennflecks

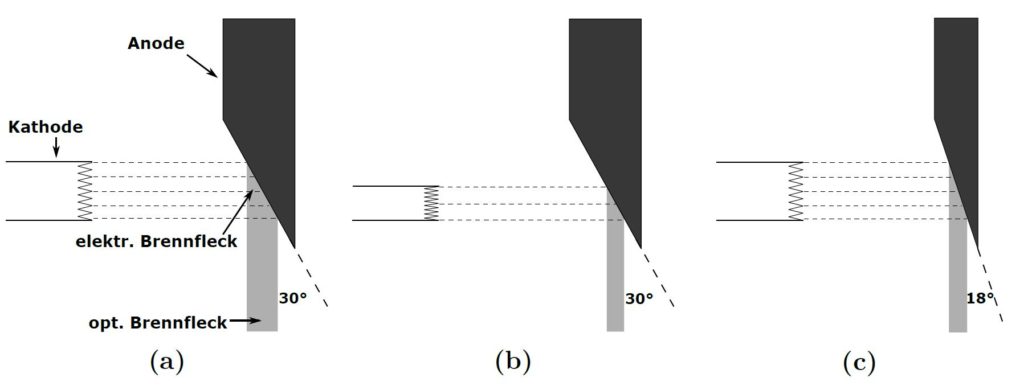
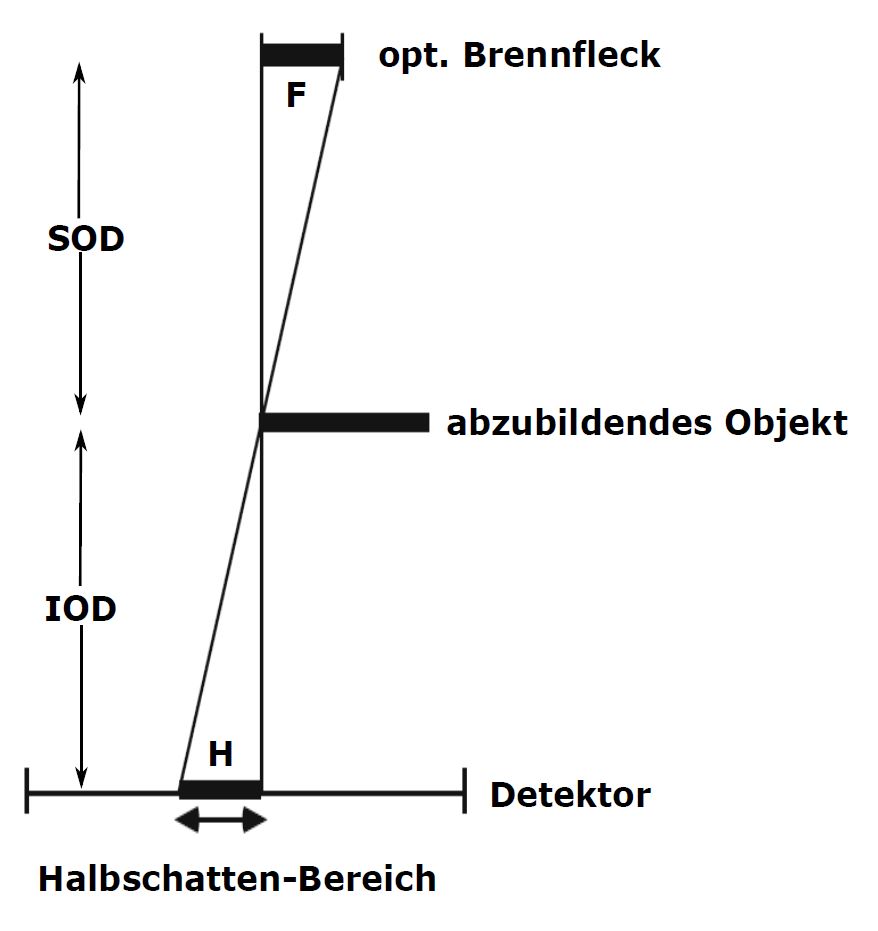
Neben einem möglichst hohen Wirkungsgrad wird die Qualität einer Röntgenquelle durch die mögliche Röntgenleistung und der Größe ihres optischen Brennflecks bestimmt. Aufgrund der räumlichen Ausdehnung des elektronischen Brennflecks (Schnittfläche von Elektronenstrahl und Anodenoberfläche) kommt es bei der Abbildung von Objekten zu sog. Halbschatteneffekten (s. Abbildung unten links), bei denen das Objekt aufgrund der Brennfleckausdehnung $F$ über den Bereich $H$ des Bildes verschmiert und so die räumliche Auflösung limitiert wird. Die Ausprägung des Effektes lässt sich mithilfe des Strahlensatzes bestimmen:

$H = F \cdot (IOD / SOD)$

wobei $SOD$ (Source-to-Object-Distance) dem Abstand zwischen Quelle und Objekt und $IOD$ (Image-to-Object-Distance) dem Abstand zwischen Bildempfänger und Objekt entspricht. Der Halbschatteneffekt ist also umso stärker, je größer die Brennfleckausdehnung ist.

Somit wäre, aus Sicht der Bildqualität, eine Minimalisierung des elektronischen Brennflecks sinnvoll. Die Verkleinerung des elektronischen Brennflecks hat jedoch zwei Nachteile:

Mit kleiner werdendem elektronischen Brennfleck steigt auch die aufgenommene Wärmeleistung pro Fläche. Um dies zu kompensieren wird die aufgenommene Wärme auf eine größere Fläche verteilt und so die Lebensdauer verlängert, in-dem die Anode zusätzlich drehbar gelagert wird (sog. Drehanoden). Typische Drehzahlen liegen bei 3.000 Umdrehungen pro Minute. Stehanoden kommen nur noch in Röntgentherapiegeräten zum Einsatz, bei denen die Verwendung eines größeren elektronischen Brennflecks aufgrund der fehlenden Bildgebung nicht nachteilig ist.
Die Größe des elektronischen Brennflecks auch direkt proportional zu der Leistung einer Röntgenröhre. Mit einer hohen Leistung können kurze Belichtungszeiten gewählt werden, wodurch Bilder seltener verwackelt und auch bewegte Organe abgebildet werden können. Somit ergibt sich ein Konflikt zwischen hoher Röntgenleistung und einer hohen Ortsauflösung. Aus diesem Grund verfügen Röntgenquellen über eine, relativ zur Elektronenbahn, schräg gestellte Anode. So ergibt sich trotz großem elektronischen Brennfleck durch dessen Projektion auf eine zum Zentralstrahl rechtwinklige Ebene ein kleiner optisch wirksamer Brennfleck (fälschlicherweise auch oft als Fokus bezeichnet), sodass eine hohe Röntgenleistung und eine gute Ortsauflösung vereinbar sind (Abbildung 7). Typische Anodenwinkel liegen zwischen 6° und 16°. Ein Nachteil schräg gestellter Anoden ist eine räumliche Verteilung der Halbschattenunschärfe in der Bildebene (Abbildung 6b). Meist werden aber nur kleine Winkelbereiche für eine Röntgenaufnahme genutzt, sodass der Effekt nicht in relevantem Maße zum Tragen kommt. Zudem kommt es bei kleineren Anodenwinkeln zu einem stärkeren Heel-Effekt und somit zu einer Aufhärtung des Röntgenspektrums (s. o.). Einige Röntgenquellen verfügen über sog. Doppel- oder Triplefokus-Anoden, die über verschieden lange Glühwendeln und/oder Anodenflächen mit unterschiedlichen Winkelbereichen verfügen, sodass je nach Anforderung zwischen hoher Leistung und hoher Auflösung umgeschaltet werden kann

Filterung

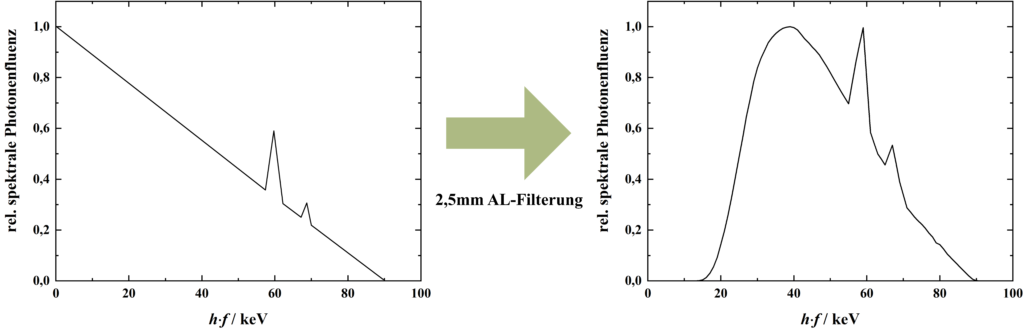
Das ungefilterte Röntgenspektrum gleicht einer Dreiecksverteilung (s. Abbildung unten). Da die niedrigen Photonenenergien (auch weiche Röntgenstrahlung genannt) aufgrund des steilen Gradienten des Wirkungsquerschnittes für den Photoeffekt $\phi_\text{Ph}$ aber in erster Linie zur Dosisbelastung des Patienten und weniger zur Bildgebung beitragen, werden diese beim Austritt aus der Röntgenröhre bestmöglich herausgefiltert. Daher besteht das Austrittsfenster typischerweise aus 1,5 mm bis 2,5 mm dickem Aluminium oder einem gleichwertigen Material. Dies wird auch als Eigenfilterung der Röntgenröhre bezeichnet. So werden die niederenergetischen Photonen durch den Photoeffekt entfernt („Aufhärtung“ des Röntgenspektrums). Für pädiatrische oder interventionelle Anwendungen werden gegebenenfalls zusätzliche Kupferfilter mit einer Stärke von bis zu 1,5 mm verwendet. Dies reduziert die Dosisbelastung des Patienten erheblich (man spricht auch von spektralem Dosismanagement), wirkt sich aber auch aufgrund der Compton-Effekt-Dominanz negativ auf die Bildqualität aus.

Einblendung und Dosismessung

Die durch das Strahlenaustrittsfenster austretende Strahlung wird Primärstrahlung genannt. Jede Röntgenquelle verfügt über eine Primärblende aus Blei direkt hinter dem Strahlenaustrittsfenster. Als Nutzstrahlung wird der Anteil der Primärstrahlung bezeichnet, der die Primärblende passiert. Zur weiteren Modulation der Nutzstrahlenfeldgröße dient eine sog. Tiefenblende. Diese besteht aus einem System verstellbarer Bleilamellen, welche in mehreren Ebenen angeordnet sind, sodass die Feldgröße an das zu untersuchende Objekt angepasst werden kann. Zur Erstellung von asymmetrischen Feldern verfügen einige Anlagen zusätzlich über keilförmige Blenden. Nach der Anpassung der Feldgröße erfolgt die Dosisüberwachung des Nutzstrahlenbündels, die nach StrSchV an allen Anlagen zur Abschätzung des stochastischen Strahlenrisikos des Patienten gefordert wird. Bei radiologischen Systemen erfolgt dies über die direkte Messung des $DFP$ mithilfe einer luftoffenen Ionisationskammer unter SEG-Bedingungen. Optional werden in einigen Fällen zusätzlich vom $DFP$ abgeleitete Größen, wie die Einfallsdosis $K_\text{E}$ oder sogar die Oberflächendosis $K_\text{O}$ für einen fest definierten Referenzpunkt im Strahlengang bestimmt.

Strahlungsfeldgrößen

Da sich der Nutzstrahl einer Röntgenröhre aus mehreren Photonenenergien zusammensetzt, ist es wichtig Größen zu definieren, mit denen sich die Strahlungsqualität, also das physikalische Verhalten des Photonenspektrums, eindeutig beschreiben lässt. Einige dieser Strahlungsfeldgrößen werden nun im Folgenden gemäß DIN 6814-2 definiert.

Teilchenfluenz

$\Phi = \text{d}N / \text{d}A$

Die Teilchenfluenz $\Phi$ ist die Teilchenanzahl $\text{d}N$ , die durch eine Kugel mit der Querschnittfläche $\text{d}A$ tritt.

Spektrale Teilchenfluenz

$\Phi_\text{E} = \text{d}\Phi / \text{d}E$

Die spektrale Teilchenfluenz $\Phi_\text{E}$ setzt die Teilchenfluenz $\Phi$ in Bezug zur Energie $E$ . $\text{d}\Phi_\text{E}$ ist dabei die Fluenz aller Teilchen, deren Energien in dem Energieintervall $E, E +\text{d}E$ liegen. Durch Aufintegration von $\text{d}\Phi_\text{E}$ über alle Energien ergibt sich wieder die Teilchenfluenz. Die spektrale Teilchenfluenz ist die Größe, die in der Regel zur Darstellung eines Photonenspektrums verwendet wird.

Energiefluenz

$\Psi = \text{d}R / \text{d}A = \bar{E} \cdot \Phi$

Die Energiefluenz $\Psi$ ist der Differentialquotient der Strahlungsenergie (Summe aller Teilchenenergien) $\text{d}R$ der Teilchen, die durch eine Kugel mit der Querschnittsfläche $\text{d}A$ treten.

Spektrale Energiefluenz

$\Psi_\text{E} = \text{d}\Psi / \text{d}E = E \cdot \Phi_\text{E}$

Die spektrale Energiefluenz $\Psi_\text{E}$ setzt die Energiefluenz $\Psi$ in Bezug zur Energie $E$ . Somit ist $\Psi_\text{E}$ die Energiefluenz aller Teilchen, deren Energien in dem Energieintervall $E, E + \text{d}E$ liegen.

Mittlere Energie

$\bar{E} = \Psi / \Phi = 1 / \Phi \cdot \int_{0}^{\infty}\Psi_\text{E} \cdot \text{d}E$

Die mittlere Energie $\bar{E}$ eines Photonenspektrums ergibt sich aus dem Quotienten aus Energiefluenz und Teilchenfluenz.

Mittlerer Schwächungskoeffizient

$\bar{\mu} = 1 / \Phi \cdot \int_{0}^{\infty}\mu(E) \cdot \Phi_\text{E} \cdot \text{d}E$

Der lineare Schwächungskoeffizient $\mu$ wird über die spektrale Teilchenfluenz gemittelt.

Mittlerer Energieübertragungskoeffizient

$\bar{\mu}_\text{tr} = 1 / \Psi \cdot \int_{0}^{\infty}\bar{\mu}_\text{tr}(E) \cdot \Psi_\text{E} \cdot \text{d}E$

Der lineare Energieübertragungskoeffizient wird über die spektrale Energiefluenz gemittelt.

Effektive Energie

Die effektive Energie ist die Energie eines monochromatischen bzw. monoenergetischen Photonenstrahls, der bzgl. eines bestimmten physikalischen Effekts dasselbe Verhalten zeigt wie das betrachtete Photonenspektrum. Beispielsweise ist die effektive Energie bezüglich der Schwächung eines Photonenspektrums die Photonenenergie, die dem über die spektrale Teilchenfluenz gemittelten Schwächungskoeffizienten entspricht.

Die Angabe der spektralen Teilchenfluenz oder der spektralen Energiefluenz legt die Strahlungsqualität eines Photonenspektrums eindeutig fest. Da die genaue Verteilung von $\Phi_\text{E}$ oder $\Psi_\text{E}$ in der Praxis oft nicht oder nur unzureichend bekannt ist, wird die Strahlungsqualität häufig mithilfe der Halbwertschichtdicke ( $HWD$ ) von Aluminium (Al) oder Kupfer (Cu) beschrieben. Diese beschreibt die Targetdicke, nach der der Primärstrahl die Hälfte seiner ursprünglichen Intensität eingebüßt hat. Sie wird üblicherweise in mm angegeben und ergibt sich aus dem Lambert‘schen Gesetz mit dem liniearen Schwächungskoeffizienten $\mu$ :

$HWD = \ln{2} / \mu$

Die $HWD$ lässt sich verglichen mit $\Phi_\text{E}$ und $\Psi_\text{E}$ sehr viel leichter messen. Bei Röntgenspektren kann es jedoch vorkommen, dass zwei Spektren mit ähnlichen $HWD$ -Werten für Aluminium unterschiedliche mittlere Schwächungskoeffizienten für das betrachtete Medium aufweisen. Aus diesem Grund ist die Angabe von Anodenspannung und Zusatzfilterung bei sonst konstanten Röhreneigenschaften (Generatorwelligkeit, Anodenwinkel und –material) zur Charakterisierung der Strahlungsqualität sehr viel genauer.

Die Strahlenqualität einer Röntgenröhre kann durch viele Faktoren beeinflusst werden. Im Folgenden sind einige der wichtigsten Einflussfaktoren und ihre Auswirkungen auf die spektrale Teilchenfluenz beschrieben.

Das Röntgenspektrum beeinflussende Parameter

Kathodenheizspannung

Die Kathodenheizspannung $U_\text{H}$ beeinflusst ausschließlich die Anzahl der beschleunigten Elektronen (Stromstärke) und somit die Teilchenfluenz des Röntgenspektrums und hat somit keinen Einfluss auf dessen Form. Durch Erhöhung von $U_\text{H}$ kann also die Teilchenfluenz erhöht und somit die nötige Belichtungsdauer herabgesetzt werden.

Anodenspannung

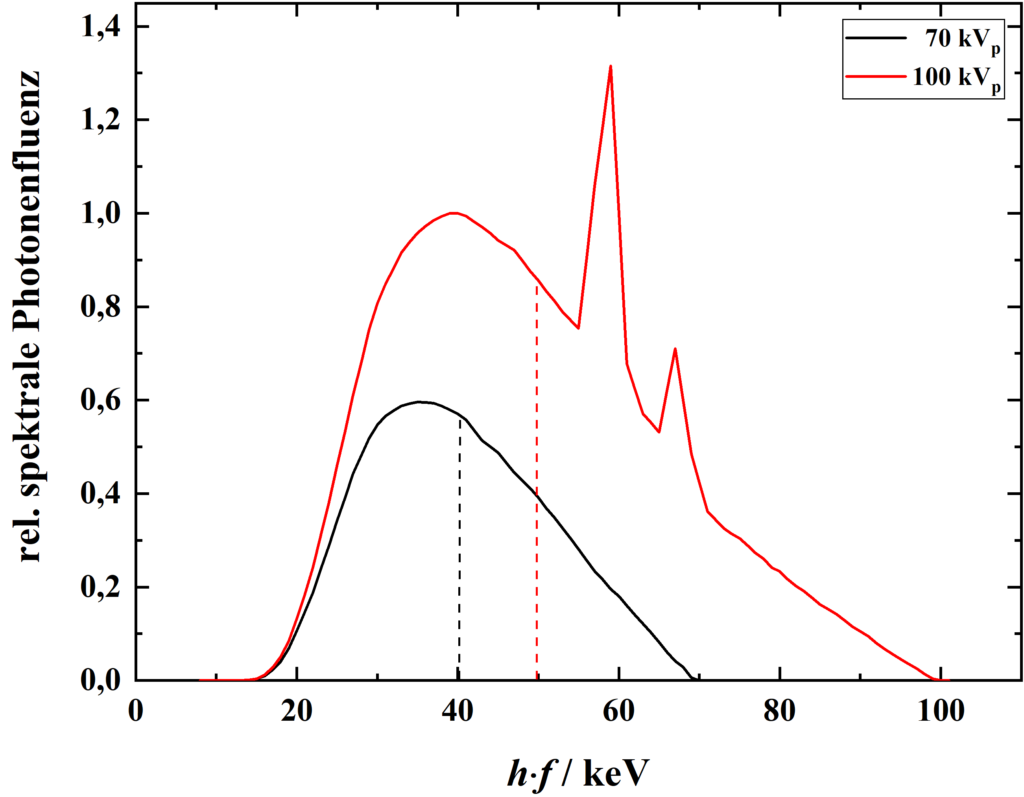
Der Einfluss der Anodenspannung $U_\text{A}$ wird in der nebenstehenden Abbildung dargestellt. Mit zunehmender Anodenspannung $U_\text{A}$ steigt aufgrund des „Durchgriffs“ auf den Röhrenstrom und der Proportionalität zwischen Anodenspannung und Wirkungsgrad die Teilchenfluenz. Zudem verschiebt sich das Bremsspektrum hin zu höheren Energien, sodass der mittlere lineare Schwächungskoeffizient sinkt. Somit können, unter Einbußen bezüglich der Bildqualität, die Heizspannung und/oder die Belichtungsdauer, sowie die Dosis reduziert werden. Auch können die Effekte zur Aufnahme von dickeren bzw. dichteren Objekten genutzt werden.

Zusatzfilterung

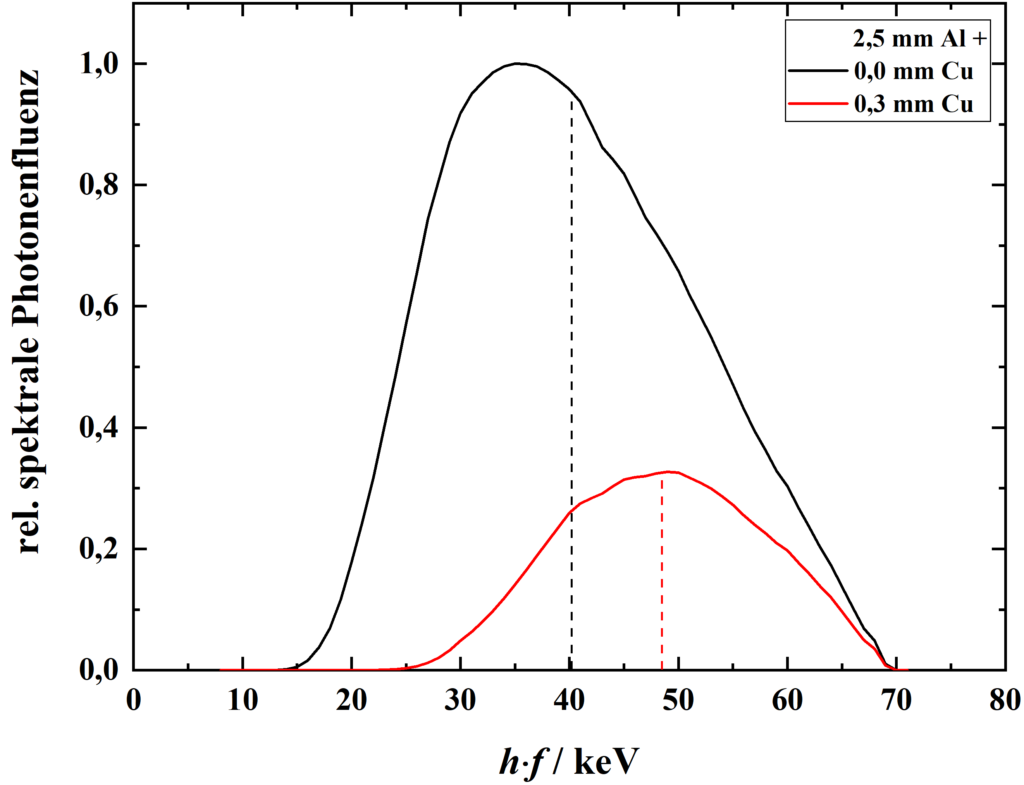
Neben größerer Anodenspannung kann auch zusätzliche Filterung ein Anstieg der mittleren Energie bewirken. Im Gegensatz zur zunehmenden Spannung verschiebt sich hier jedoch nicht das gesamte Spektrum zu höheren Energien. Vielmehr wird es durch das zusätzliche Filtermaterial geschwächt. Da der lineare Schwächungskoeffizient für niedrigere Energien höher ist als für größere, werden diese im Verhältnis stärker abgeschwächt. Somit steigt die mittlere Energie des Spektrums während der mittlere Schwächungskoeffizient sinkt, ohne dass dabei die maximale Photonenenergie angehoben wird. Dieser Prozess wird als „Aufhärtung“ des Spektrums bezeichnet. So kann insbesondere bei dünneren oder weniger dichten Objekten Dosis eingespart werden. Der damit verbundene Verlust der Bildqualität ist nicht so groß wie bei der Erhöhung der Anodenspannung. Jedoch muss aufgrund der erheblichen Verminderung der Teilchenfluenz die Heizspannung und/oder die Belichtungsdauer heraufgesetzt werden. Typischerweise werden zur Zusatzfilterung Aluminium- oder Kupferplatten verwendet.

Generatorwelligkeit (ripple)

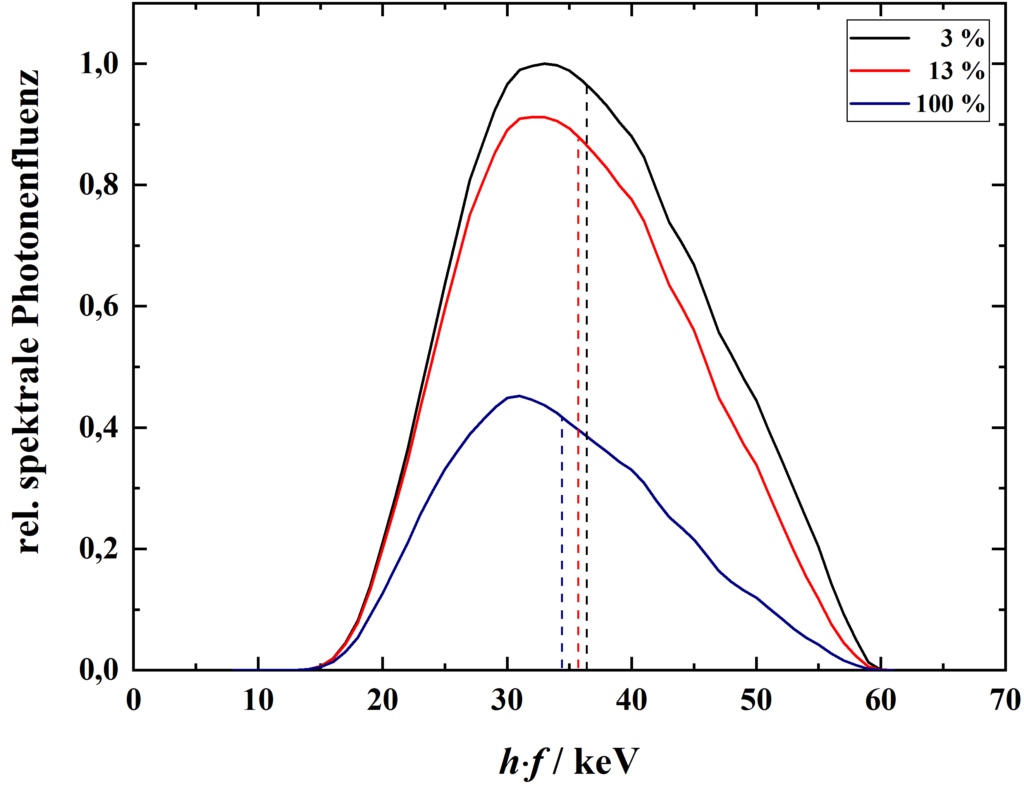
Die Generatorwelligkeit wirkt sich in erster Linie auf die Teilchenfluenz aus. Diese sinkt mit steigender Welligkeit erheblich, sodass eine höhere Heizspannung und/oder Belichtungsdauer erforderlich wird. Auch kommt es aufgrund des Auftretens niedrigerer Anodenspannungen bei höheren Welligkeiten zu einer leichten Verringerung der mittleren Energie und somit zu einem Anstieg des mittleren linearen Schwächungskoeffizienten. Dies muss bei der Verwendung solcher Generatortypen berücksichtigt werden. In modernen Röntgenanlagen werden jedoch nur noch 12-Puls- oder Hochfrequenzgeneratoren verwendet, deren Restwelligkeiten unter 3 % liegen.

Anodenwinkel

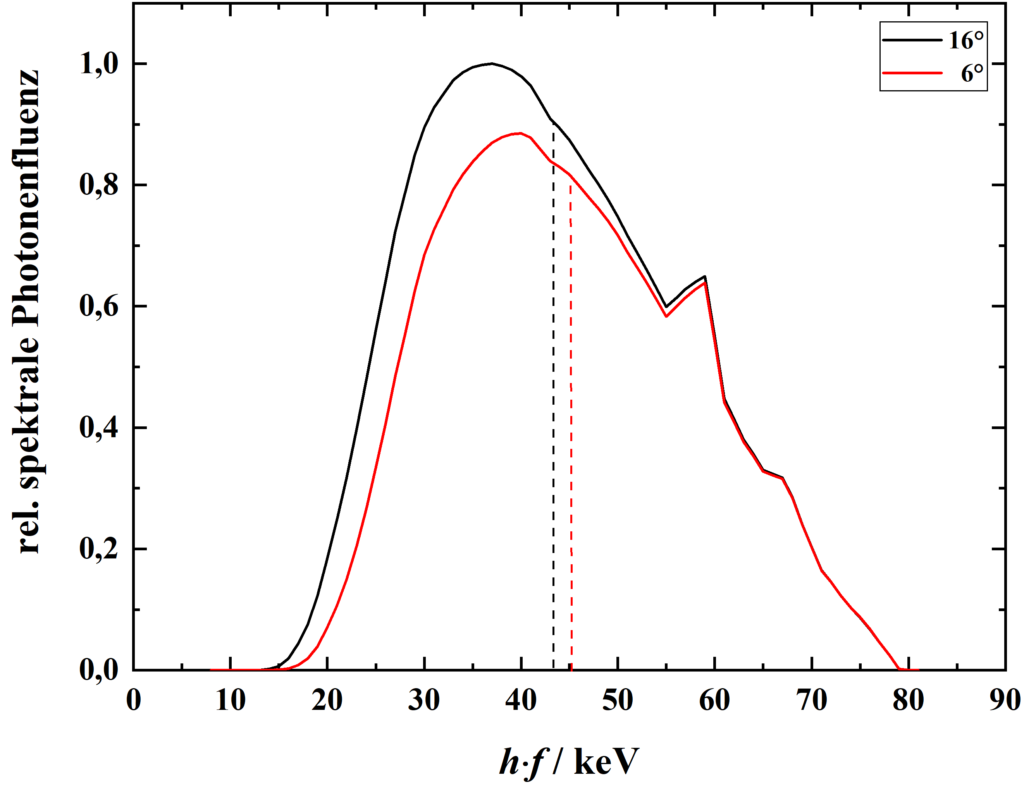
Ein kleinerer Anodenwinkel bewirkt neben der Verkleinerung des optisch wirksamen Brennflecks und der damit verbundenen Verbesserung der Auflösung eine leichte Aufhärtung des Röntgenspektrums. Aufgrund des kleineren Winkels kommt es zu einem verstärkten Heel-Effekt. Somit legen einige Photonen einen längeren Weg im Anodenmaterial zurück, sodass die Anode an Filtereigenschaften gewinnt. Folglich kommt es zu einem Absinken der Teilchenfluenz und des mittleren Schwächungskoeffizienten und zu einem Anstieg der mittleren Energie. Auch dies muss beim Betrieb berücksichtigt werden. Zudem kann es bei längerer Verwendung aufgrund der zunehmenden Aufrauhung der Anodenoberfläche zu einer Erhöhung der $HWD$ des Photonenspektrums von bis zu 10 % gegenüber dem Ausgangswert kommen (DIN 6809-3. Klinische Dosimetrie – Röntgendiagnostik. Deutsches Institut für Normung e. V., 1990.).

Röntgenröhre

Inhaltsverzeichnis